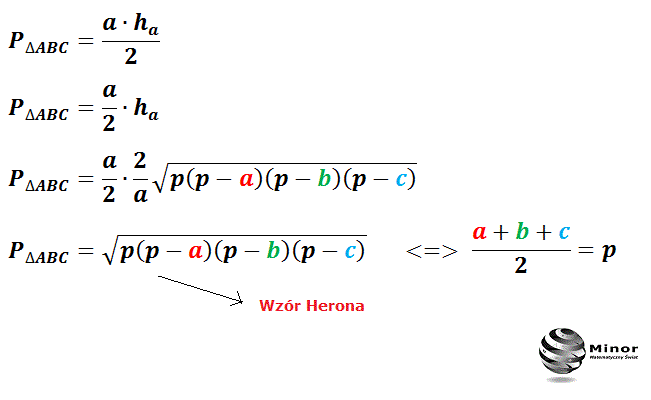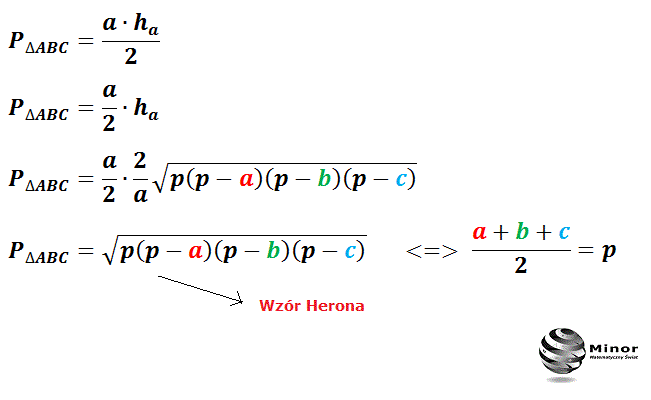Wzór Herona – wzór pozwalający obliczyć pole (S) trójkąta, jeśli znane są długości a, b, c jego boków. Wzór znany był już Archimedesowi, a jego nazwa pochodzi od Herona, który podał go w swojej Metryce.
Niech oznacza połowę obwodu trójkąta. Wtedy jego pole S wynosi:
Wzór Herona może zostać wykorzystany do obliczeń, nawet jeżeli odcinki o podanych długościach nie tworzą trójkąta. W sytuacji, gdy wszystkie trzy odcinki i wszystkie trzy łączące je punkty leżą na jednej prostej, na przykład, gdy zachodzi równość więc wyrażenie jest równe co powoduje, że
Jeżeli natomiast odcinkami o podanych długościach nie można połączyć trzech punktów tej samej płaszczyzny, tzn. to wartość co sprawia, że wyrażenie pod pierwiastkiem jest ujemne, a więc
Dowód
W dowodzie wykorzystamy inny wzór na pole trójkąta
W tym celu, korzystając z twierdzenia cosinusów, wyznaczmy wartość kwadratu cosinusa kąta
Korzystając z jedynki trygonometrycznej i przekształceń algebraicznych, otrzymujemy:
oznacza połowę obwodu trójkąta, więc
Podstawiając otrzymany wynik do wymienionego na początku wyrażenia, otrzymujemy wzór Herona.
Postać wyznacznikowa
Wzór na pole z wykorzystaniem wysokości
Jeśli są wysokościami trójkąta o bokach odpowiednio to Po podstawieniu tych wzorów do wzoru Herona i prostych przekształceniach otrzymujemy:
Wzór Brahmagupty
Wzór Brahmagupty to wzór analogiczny do wzoru Herona, który pozwala obliczyć pole S czworokąta o bokach długości wpisanego w okrąg:
gdzie:
oznacza połowę obwodu czworokąta.
Dla dowolnego czworokąta (również niewpisanego w okrąg), wzór na jego pole przedstawia się następująco:
gdzie to połowa sumy dowolnej pary dwóch przeciwległych kątów czworokąta. W przypadku czworokątów wpisanych w okrąg obie te sumy są sobie równe i wynoszą 180°.
Przypisy
Linki zewnętrzne
- JoannaJ. Jaszuńska JoannaJ., Heron uogólniony?, „Delta”, marzec 2014, ISSN 0137-3005 [dostęp 2024-10-30] .
- Eric W.E.W. Weisstein Eric W.E.W., Heron’s Formula, [w:] MathWorld, Wolfram Research [dostęp 2020-12-12] (ang.).
- Eric W.E.W. Weisstein Eric W.E.W., Brahmagupta’s Formula, [w:] MathWorld, Wolfram Research [dostęp 2020-12-12] (ang.).